MMD on WebGL 踊れるようになった（あと IK について）

IK を実装して踊れるようになった。

11月2日現在、「きしめん」を踊ってくれる。普通のスピードで再生できれば25秒ぐらい。

http://edv.sakura.ne.jp/mmd/

MMD のフレームは 30fps なので、リアルタイムに再生するなら 1000ms/30=33ms ぐらいで1フレームの処理を終えなければならないのだけど、IK の計算で 30ms ぐらいかかってしまう時もあり（GC のためか）、物理演算までやるのは厳しくなってきた。今でさえちょっと遅いパソコンだとスローモーションになってしまう。あと Firefox より Chrome のほうがかなり速い。

Lat 式から頂点数の少ないモブ子さんに替えてみた。Firefox でもヌルヌル動くはず。ただし Windows の Firefox にはバグがあるので真っ白になることもある。

物理までやったらもうちょっと最適化してみる。

IK について

↓この動画の5分40秒目以降を先に見たほうが理解しやすいはず。

【ゆっくり解説】第8回 MMDモデルを踊らす【3Dプログラミング】 ‐ ニコニコ動画(原宿)

以下は主に数式の説明になる。前回の Forward Kinematics の説明と一部かぶるところがある。

IK 演算に関係するボーンはこんな感じになっている。（IK 影響下のボーンは平行移動はしないみたいなので考えないことにする）

ボーン名	タイプ	位置	個別回転	合成回転
センター	回転・移動	$P_C$	$R_C$	$R_C$
...	...	...	...	...
右髪１	回転	$P_5$	$R_5$	$\tilde{R}_5$
右髪２	IK影響下	$P_4$	$R_4$	$\tilde{R}_4$
右髪３	IK影響下	$P_3$	$R_3$	$\tilde{R}_3$
右髪４	IK影響下	$P_2$	$R_2$	$\tilde{R}_2$
右髪５	IK影響下	$P_1$	$R_1$	$\tilde{R}_1$
右髪６	IK影響下	$P_0$	$R_0$	$\tilde{R}_0$
右髪７	IK接続先	$P_T$	...	...
右髪ＩＫ	IK	$P_I$	...	...
右髪ＩＫ先	非表示	...	...	...

「個別回転」というのは VMD ファイルから得られる数字で、モデルの初期姿勢からのそのボーンの回転をグローバル座標で表したもの（他の 3D のフォーマットではボーンのローカル座標で回転・平行移動表すこともあるらしい）。「合成回転」というのは各ボーンの親からの回転を順々に掛けていったもので、これも当然グローバル座標。

例えば「右髪６」の合成回転を求めるには、

${\large \tilde{R}_0 = \tilde{R}_1 R_0 = \tilde{R}_2 R_1 R_0 = \tilde{R}_3 R_2 R_1 R_0 = \dots }$

のようにしてセンターから順に回転を掛けていけばいい。

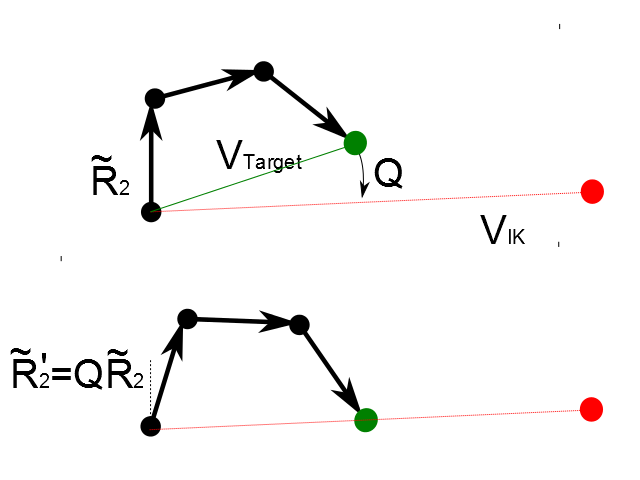
下の図で、緑は「右髪７」に、黒は先から順に「右髪６」「右髪５」…にそれぞれ対応する。一番左が初期位置で、真ん中は一番先の回転を適用したところ、次は二番目の回転を適用したところ、となっている。

そうやってまず Forward Kinematics 計算をする。ちなみに「右髪７」までは上からずっと親子関係になってて、「右髪ＩＫ」はセンターの直接の子になっている（足の IK はセンターの子ですらない）。「右髪ＩＫ先」は計算には関係ないので気にしなくていい。

さて、IK 接続先（IK ターゲットと呼ばれることのほうが多いかも）である「右髪７」までの合成回転と合成位置を求めた後で、IK 影響下のボーンのうち一番先端である「右髪６」に注目する。

「右髪６」から IK ターゲットである「右髪７」までのベクトル ${\bf V_T}$ と、「右髪６」から IK ボーンである「右髪ＩＫ」までのベクトル ${\bf V_I}$ を求め、「右髪７」の位置が「右髪６」と「右髪ＩＫ」を結んだ線上に来るような回転 $Q$ を求める。

赤い点は IK ボーン。

回転 $Q$ は回転軸 ${\bf a}$ と回転角 $\theta$ から求められ、それぞれ

${\large {\bf a} = \frac{ {\bf V}_T \times {\bf V}_I }{ \| {\bf V}_T \times {\bf V}_I \| } }$
${\large \theta = \frac{ \| {\bf V}_T \times {\bf V}_I \| }{ \| {\bf V}_T \| \| {\bf V}_I \| } \,\,\, \mathrm{when} \,\,\, {\bf V}_T \cdot {\bf V}_I \ge 0 \,\,\, \mathrm{or} \,\,\, \theta = \pi - \frac{ \| {\bf V}_T \times {\bf V}_I \| }{ \| {\bf V}_T \| \| {\bf V}_I \| } \,\,\, \mathrm{when} \,\,\, {\bf V}_T \cdot {\bf V}_I \lt 0 }$

となる。（ $0 \le \theta \le \pi$ しか考えなくてもいい。なぜならそれ以上の角度のときは回転軸が逆向きになるだけだからである。）

「右髪６」の合成回転 $\tilde{R}_0$ に先ほど求めた $Q$ を掛けて修正合成回転 $\tilde{R}'_0$ とする。この $\tilde{R}'_0$ を使ってターゲットである「右髪７」の新しい位置を計算して終わり。

同じようにして順に「右髪５」「右髪４」等についても計算する。「右髪５」の修正合成回転を求めた後はまた「右髪６」「右髪７」の順に新しい位置を計算していく必要がある。「右髪４」の時は「右髪５」「右髪６」「右髪７」という順。

これを IK 影響下の一番根元である「右髪２」までやり、次はまた「右髪６」から、という具合に PMD ファイルで指定された回数繰り返す。

以上で、実は二点端折ったところがある。まず、MMD の IK にはそれぞれ「一回のステップで一つのボーンが曲がれる角度制限（単位制限角）」がある。

極北Pさんの PMDEditor の Readme （一番下に引用した）の説明によると、指定された値×4 radian までしか曲がれないらしい。なので、上で $\theta$ を求めたときに、この単位制限角との max を取る必要がある。

もう一つのポイントは、「ひざ」という名の付くボーンは X 軸方向にしか動かないというもの。（PMX だと好きなボーンに角度制限が付けられるらしいが）

これをやるにはちょっと面倒なことをしないといけない。なぜなら、先ほど求めた $\tilde{R}'_0$ などは、いわば「修正『合成』回転」になるため、そこから「修正『個別』回転」 $R'_0$ を求め、これに角度制限をかけ、さらにそれを合成回転に直さないといけない。（回転軸制限は個別回転に適用されるもので、合成回転にではない）

$\tilde{R}'_0 = Q \tilde{R}_0$ （修正合成回転は合成回転に $Q$ を掛けたもの）と $\tilde{R}'_0 = \tilde{R}_1 R'_0$ （修正合成回転は修正個別回転に親ボーンの合成回転を掛けたもの）を組み合わせると、

${\large \tilde{R}'_0 = \tilde{R}_1 R'_0 = Q \tilde{R}_0 }$
${\large \Downarrow }$
${\large R'_0 = \tilde{R}_1^* Q \tilde{R}_0 }$

となる。（両辺に $\tilde{R}_1$ の逆元 $\tilde{R}_1^*$ をかけた）

$R'_0$ は親の回転を加味しない絶対的なものなので、これの Y 軸方向と Z 軸方向の回転をゼロにして X 軸方向の回転をそのぶん増やしてやれば、「ひざ」の「制限付き修正個別回転」 $R''_0$ が求められる。

「制限付き修正合成回転」は単に親の合成回転を掛ければいいだけなので

${\large \tilde{R}''_0 = \tilde{R}_1 R''_0 }$

となる。

以上のプロセスを、ボーンの位置を逆から求めていくので Inverse Kinematics (IK) と呼ぶ。上の方法だけが唯一の IK の計算方法というわけではない。検索してみたら別の方法もあるらしい。ただ、PMD ファイルの「単位制限角」や「ループ回数」というパラメーターを使うなら上の方法しかないと思う。

以下は参考にならないかもしれないけどイメージを膨らませるのにはいい。

PMDEditor 0.0.9.9 の Readme.txt より引用

●[IK]
IKリスト : IKボーンとして機能するボーンの一覧。
→
IK(数値)           : 対応するIKボーンIndex
Target(数値)       : IKボーンの位置にこのボーンを一致させるようにIK処理が行われる
IKループ回数(整数) : IK処理での計算回数(最大255)
単位制限角(実数)   : 一回のIK計算での制限角度(数値はrad値の模様? | 1.0=4[rad](230度程度) 180度:0.7854 = 3.141592/4)
影響下ボーンリスト : IKの影響下にあるボーン一覧 | IK接続先に近い方からリスト順にする必要がある

※各関連値は[ボーン]側で設定されている項目もありますが、IKリストはボーンリストとは独立して必要。

※IK処理においては、特定の制限角度がボーン名に従ってMMD側で調整されるようです。
例：ひざ→縦(X軸方向)にしか稼動しない


○degボタン
単位制限角を角度で入力／有効範囲は0-180後程度(あくまで解析情報からの推測値となります)


○IK値(IKループ回数／単位制限角)について
IK値によるIKの制御パラメータの関係について、大体以下のようになるようです。

<IKループ回数>, <単位制限角>
小, 大 : IKのLink先ボーンに強く依存する＝先だけよく曲がる(系列が短い場合はこれで十分)
大, 小 : IK系列全体で曲がるようになる(しなりが強くなり直線形状になりやすい)

大, 大 : 比較的 (小, 大) と同様の傾向を示すと思われる。
小, 小 : 非常に曲がりにくくなり、IKに対する追従も悪くなる

多くのボーン系列を持つような場合は、単位制限角を非常に小さな値にする必要がある。

単位制限角による制限はIK影響下ボーンが下位に進むにつれ(ボーン列的には根元に行くになるに従って)、
制限角度が拡がっていく仕様なので、多関節の場合、先端付近より根元の方が比較して大きく曲がるようになる。

※IK変形は通常のボーン変形に比べ繰り返し回数がかなり多いので、非常に負荷の高い変形になります。